21. Scipy Tutorial-图像旋转变换

scipy的misc模块里提供了很多的内建图像数据，例如lena、face、ascent等，可供在scipy里直接访问这些图像数据并使用scipy提供的一些算法处理;scipy的ndimage模块里也有一些函数可以对scipy图像数据进行操作例如旋转函数rotate可以以任意角度旋转图像。无论怎样，图像数据在scipy、opencv里等都是一数组的形式存在，灰度图是二维的，而彩色图像数据是三维的，所以图像在scipy、numpy或者python里都是数组，那么在之前的章节NumPy矩阵的旋转研究了用自己的办法去旋转矩阵或者方阵，那么在scipy、Numpy里图像本质是数组，那么也可用NumPy矩阵的旋转章节里的方式去旋转图像！

本章简要介绍scipy.ndimage里的rotate函数，去旋转图像，本章还想再次尝试NumPy矩阵的旋转一章里的方法去旋转图像，看行不行？

21.1 ndimage.rotate旋转图像

scipy.ndimage里的rotate函数能旋转图像，功能挺强！

scipy.ndimage.rotate(input, angle, axes=(1, 0), reshape=True, output=None, order=3, mode='constant', cval=0.0, prefilter=True)

参数很多，angle需要说明，正数逆时针(向左)旋转，负数时顺时针(向右)旋转。

#coding:utf-8
from scipy import misc, ndimage
import matplotlib.pyplot as plt
import scipy
print "scipy version is:", scipy.__version__

src = misc.face()
misc.imsave('faceRGB.png', src)
img = ndimage.imread("faceRGB.png", mode = "L")
misc.imsave('faceGray.png', img)
plt.gray()
plt.subplot(221, title = "org"); plt.imshow(img)
plt.subplot(222, title = "right 90"); plt.imshow(ndimage.rotate(img, -90))
plt.subplot(223, title = "left 90"); plt.imshow(ndimage.rotate(img, 90))
plt.subplot(224, title = "rotate 180"); plt.imshow(ndimage.rotate(img, 180))
plt.show()

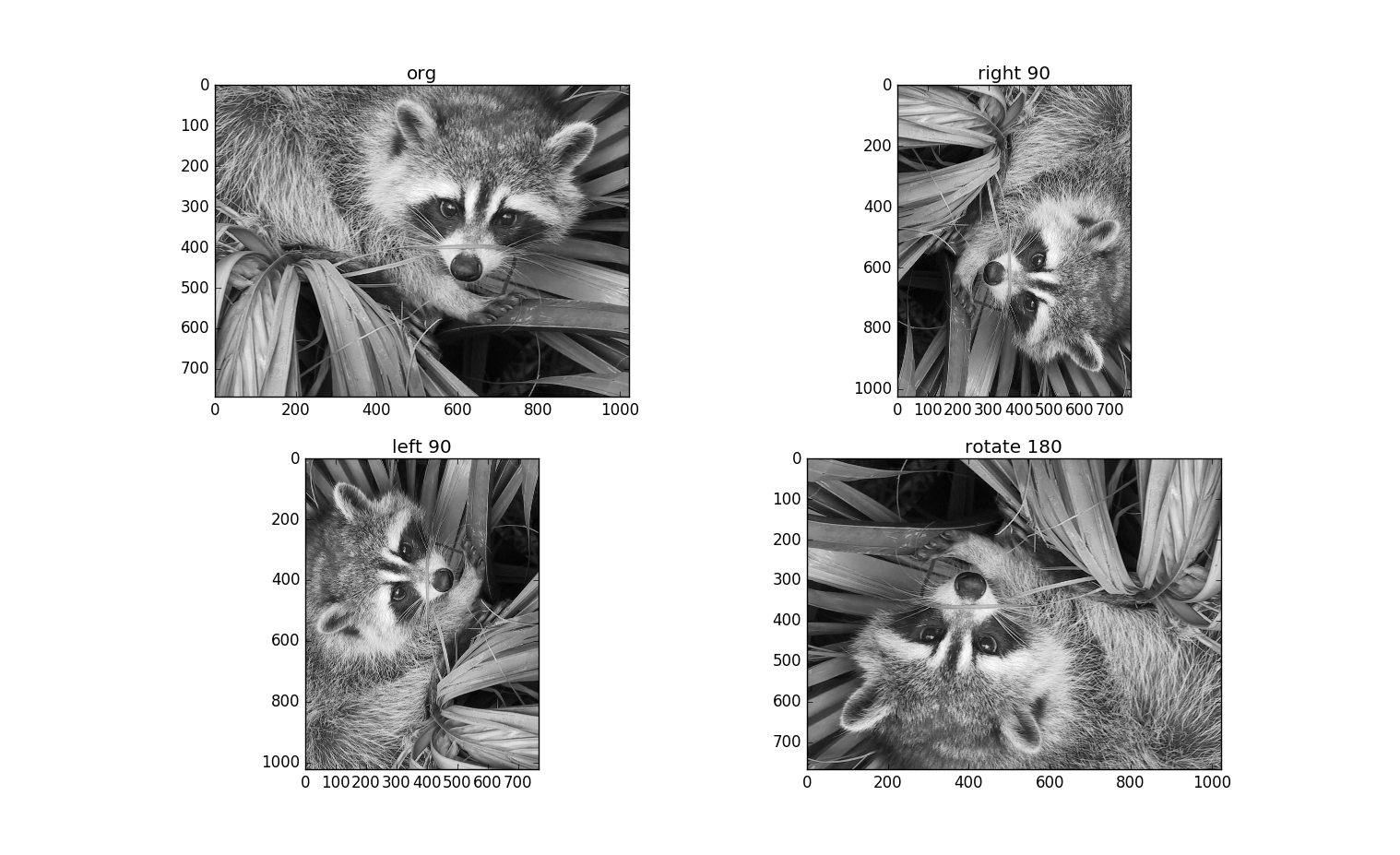scipy.ndimage.rotate函数的牛A之处在于可以任意角度旋转！很厉害！

21.2 矩阵旋转图像

参考章节NumPy矩阵的旋转里提及的方法，对矩阵左乘、右乘一个负对角线为1,其他为0的方阵(记作为：$E^{-1}$)，可以实现对图像数据的行列、旋转的变化，但此处的图像的数据不一定是方阵，在章节NumPy矩阵的旋转里提出了一个办法即先将图像扩充方阵、旋转、切片得到最后原数据的旋转数据，方法有点笨，其实有更一般的办法，和Numpy部分的13.2 Python实现方阵的旋转各节标题一致。更一般的规则如下：

$\bigotimes\ $对矩阵$A$左乘$E^{-1}$行交换，左乘需满足矩阵乘法规则即可，即矩阵$A_{m\times n}$左乘的$E^{-1}$的行列均应为$m$,即$E_{m\times m}^{-1}$。

$\bigotimes\ $对矩阵$A$右乘$E^{-1}$列交换，右乘需满足矩阵乘法规则即可，即矩阵$A_{m\times n}$右乘的$E^{-1}$的行列均应为$n$,即$E_{n\times n}^{-1}$。

$\bigotimes\ $对矩阵$A$的转置$A^{T}$左乘$E^{-1}$实现逆时针旋转$90^{\circ}$，左乘需满足矩阵乘法规则即可，即矩阵$A_{m\times n}$的转置$A_{n\times m}^{T}$左乘的$E^{-1}$的行列均应为$n$,即$E_{n\times n}^{-1}$。

$\bigotimes\ $对矩阵$A$的转置$A^{T}$右乘$E^{-1}$实现顺时针旋转$90^{\circ}$，右乘需满足矩阵乘法规则即可，即矩阵$A_{m\times n}$的转置$A_{n\times m}^{T}$右乘的$E^{-1}$的行列均应为$n$,即$E_{m\times m}^{-1}$。

$\bigotimes\ $对矩阵$A$左右各乘一个$E^{-1}$实现$180^{\circ}$的旋转，则矩阵$A_{m\times n}$左乘的$E^{-1}$的行列均应为$m$,即$E_{m\times m}^{-1}$。矩阵$A_{m\times n}$右乘的$E^{-1}$的行列均应为$n$,即$E_{n\times n}^{-1}$。

$\circ\ $这样需要获得矩阵的行列数，然后用这行列数构造两个$E^{-1}$分别为$E_{m\times m}^{-1}$和$E_{n\times n}^{-1}$，然后即可实现对图像的旋转和镜像了。

#coding:utf-8
import numpy as np

from scipy import misc, ndimage
import matplotlib.pyplot as plt
import scipy
print "scipy version is:", scipy.__version__

src = misc.face()
misc.imsave('faceRGB.png', src)
img = ndimage.imread("faceRGB.png", mode = "L")
misc.imsave('faceGray.png', img)

r, c = img.shape
print r, c
e_1_r = np.eye(r)[:,::-1]
print e_1_r
e_1_c = np.eye(c)[:,::-1]
print e_1_c

plt.gray()
plt.subplot(231, title = "org"); plt.imshow(img)
plt.subplot(236, title = "clockwise 90$^\circ \curvearrowright$"); plt.imshow(img.T.dot(e_1_r))
plt.subplot(233, title = "anti-clockwise 90$^\circ\curvearrowleft$"); plt.imshow(e_1_c.dot(img.T))
plt.subplot(232, title = "horizontal mirror $\leftrightarrow$"); plt.imshow(img.dot(e_1_c))
plt.subplot(234, title = "vertical mirror $\updownarrow$"); plt.imshow(e_1_r.dot(img))
plt.subplot(235, title = "rotate 180$^\circ \circlearrowleft$"); plt.imshow(e_1_r.dot(img).dot(e_1_c))
plt.show()

程序执行结果如下：

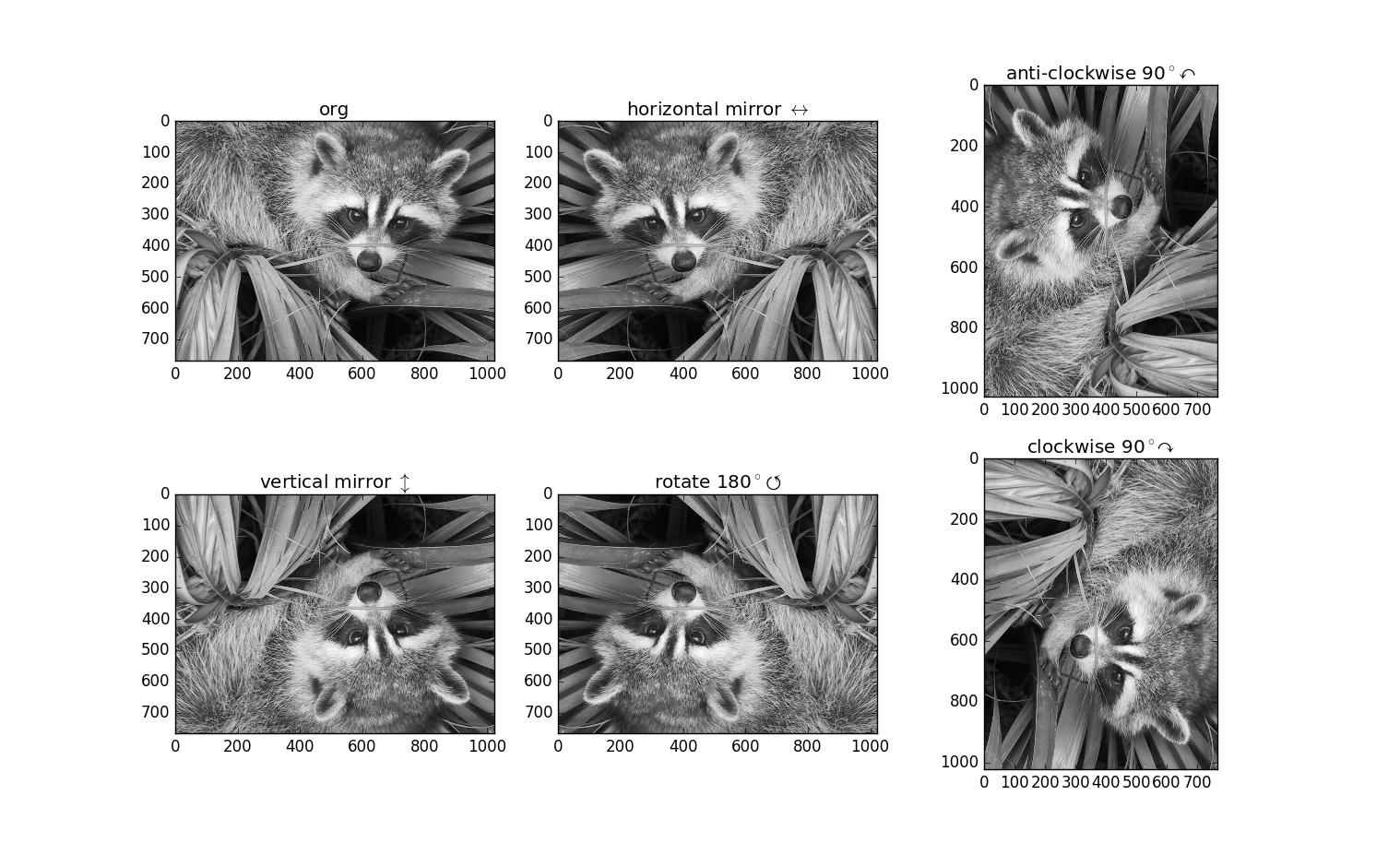解析一下程序：

(1). 获得图片的行列数

r, c = img.shape

本图图像img的行r为768、列c为1024。并构造两个$E^{-1}$即$E_{768\times 768}^{-1}$和$E_{1024\times 1024}^{-1}$。

e_1_r = np.eye(r)[:,::-1]
e_1_c = np.eye(c)[:,::-1]

(2). 图像$img_{768\times 1024}$左乘$E_{768\times 768}^{-1}$可以得到垂直镜像的$vertical\ mirror$图像。

plt.subplot(234, title = "vertical mirror $\updownarrow$")
plt.imshow(e_1_r.dot(img))

(3). 图像$img_{768\times 1024}$右乘$E_{1024\times 1024}^{-1}$可以得到水平镜像的$horizontal\ mirror$图像。

plt.subplot(232, title = "horizontal mirror $\leftrightarrow$")
plt.imshow(img.dot(e_1_c))

(4). 图像$img_{768\times 1024}$左乘$E_{768\times 768}^{-1}$、右乘$E_{1024\times 1024}^{-1}$可以得到水平镜像的$rotate\ 180^\circ$图像。

plt.subplot(235, title = "rotate 180$^\circ \circlearrowleft$")
plt.imshow(e_1_r.dot(img).dot(e_1_c))

(5). 图像$img_{768\times 1024}$的转置$img_{1024\times 768}^{T}$左乘$E_{1024\times 1024}^{-1}$可以得到逆时针$90^{\circ}$旋转的$anti-clockwise\ 90^{\circ\curvearrowleft}$图像。

plt.subplot(233, title = "anti-clockwise 90$^\circ\curvearrowleft$")
plt.imshow(e_1_c.dot(img.T))

(6). 图像$img_{768\times 1024}$的转置$img_{1024\times 768}^{T}$右乘$E_{768\times 768}^{-1}$可以得到顺时针旋转$90^{\circ}$的$clockwise 90^\circ \curvearrowright$图像。

plt.subplot(236, title = "clockwise 90$^\circ \curvearrowright$")
plt.imshow(img.T.dot(e_1_r))

21.3 图像变换总结

$\bigotimes\ $对$A$左乘$E^{-1}$行换(垂直镜像)、右乘$E^{-1}$列换(水平镜像)，左右乘$E^{-1}$旋转$ 180^\circ$。

$\bigotimes\ $对$A$的转置$A^{T}$左乘$E^{-1}$逆时针旋转$90^{\circ}$、右乘$E^{-1}$顺时针旋转$90^{\circ}$，左右乘$E^{-1}$负对角线镜像。

$\bigotimes\ $看来《线性代数》和《矩阵分析》得好好再学一下！

感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持！