18. SciPy求函数的积分

本章研究的主题是SciPy下实现求函数的积分的函数的基本使用。 积分，高等数学里有大量的讲述，基本意思就是求曲线下面积之和。 $$I(f) \approx \sum_{i = 1}^{n} w_i f(x_i) + r_n$$其中$r_n$可认为是偏差，一般可以忽略不计，$w_i$可以视为权重。 在SciPy里提供了很多的求各类积分的函数，依据传入参数的不同可以分为两类：一类是传入一个已知的函数和积分的上下限;另一类是传入点集，这个适用于做完物理实现后收集的一些数据，但函数无法确定，但有很多的数据点，那么这些点包络下的面积是多少，也是积分问题，所以在SciPy里有针对点集求积分的函数，形式上函数的参数是数组或者列表。

18.1已知函数型求积分

本节以几个问题的形式展示SciPy下如何求积分。

  • 问题1：这里假设函数为$f(x) = x + 1$,求积分的上下限为$[1, 2]$,数学表达式为： $$ I(f) = \int_1^2 (x + 1) dx $$ 可以利用Scipy模块下的子模块integrate里的quad函数来求这个数学问题的计算值。
from scipy import integrate
def f(x):
    return x + 1
v, err = integrate.quad(f, 1, 2)
print v

程序的执行结果为：

2.5

为何？我们用高等数学计算一下，看看结果和手算是否一致？ $$ I(f) = \int_1^2 (x + 1) dx = (\frac{1}{2}x ^2 + x)_1^2 =( \frac{1}{2} \times2^2 + 2) -( \frac{1}{2} \times1^2 + 1 ) = 4 - 1.5 = 2.5 $$ 计算结果和用SciPy程序运行结果一致。

  • 问题2：但对于$f(x) = ax + b$这种函数，$a$和$b$肯能未知的这种函数，quad能用么？答案是可以的，quad有形参args可以传入一些参数进去的。
from scipy import integrate
def f(x, a, b):
    return a * x + b
v, err = integrate.quad(f, 1, 2, args = (-1, 1))
print v

程序的执行结果是：

-0.5

可以看出(-1, 1)赋值给了f函数的a和b变量。用高等数学计算一下结果的正确性，此时的$f(x) = -x + 1$,那么： $$ I(f) =\int_1^2 (-x + 1) dx = (-\frac{1}{2}x ^2 + x)_1^2 = (-\frac{1}{2}\times 4 + 2) - (-\frac{1}{2} + 1) = -0.5 $$

  • 问题3：如果遇到积分函数有断点，可以通过quad函数的points给出断点继续求积分。例如： $$ I(f) = \int_{-1}^{1} \frac{1}{\sqrt |x|}dx $$ 这里的$f(x) = \frac{1}{\sqrt |x|}$在$x = 0$的地方存在断点，如果没有给出断点就通过quad计算计算：
from scipy import integrate
import numpy as np
def f(x):
    return 1 / np.sqrt(abs(x))
v, err = integrate.quad(f, -1, 1)
print v

程序运行时：

scipy1801.py:4: RuntimeWarning: divide by zero encountered in double_scalars
  return 1 / np.sqrt(abs(x))
inf

结果是inf(无限、无穷)且有除0错误！ 修改一下：

from scipy import integrate
import numpy as np
def f(x):
    return 1 / np.sqrt(abs(x))
v, err = integrate.quad(f, -1, 1, points=[0])
print v

结果是：

4

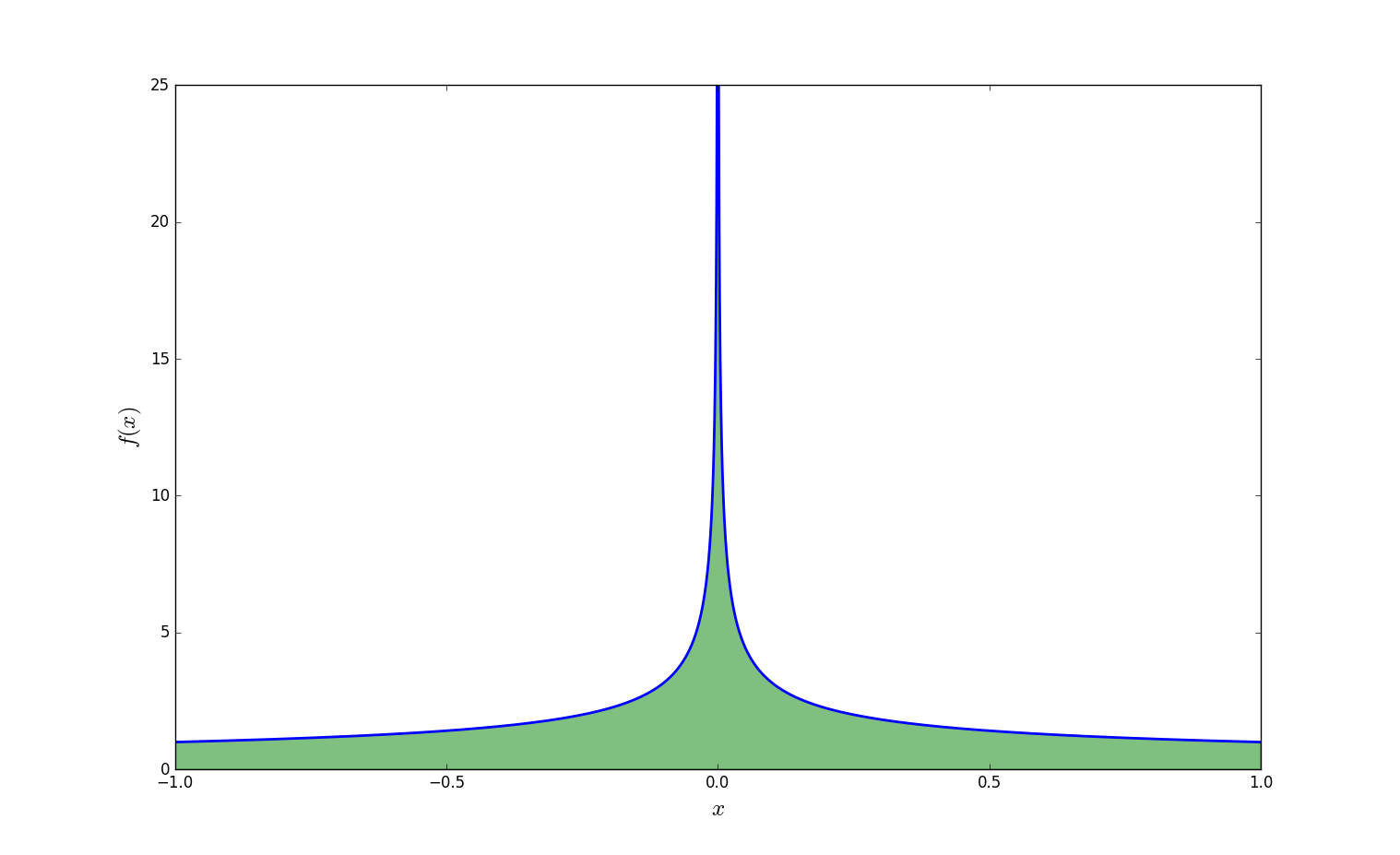
我们可以绘制一下这个函数的可视化曲线：

from scipy import integrate
import numpy as np
def f(x):
    return 1 / np.sqrt(abs(x))
v, err = integrate.quad(f, -1, 1, points=[0])
print v

import numpy as np, matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
fig, ax = plt.subplots(figsize=(8, 3))
x = np.linspace(-1, 1, 10000)
ax.plot(x, f(x), lw=2)
ax.fill_between(x, f(x), color='green', alpha=0.5)
ax.set_xlabel("$x$", fontsize=18)
ax.set_ylabel("$f(x)$", fontsize=18)
ax.set_ylim(0, 25)
plt.show()

得到如下的结果图：

18.2 给出点集的积分

在无法确认积分函数的情况下，给出一些序列也可做积分。

  • 问题4：求积分$I(f) = \int_{0}^{2} \sqrt xdx$，假设$\sqrt x$函数并不知道，而是有这个函数的10个样本数据，那传入quad函数的不是$f(x) = \sqrt x$， 而是对应的各个$(x_i, y_i)$。
from scipy import integrate
import numpy as np
def f(x):
    return np.sqrt(x)
x = np.linspace(0, 2, 10)
y = f(x)
v = integrate.trapz(y, x)
print v

程序的运行结果：

1.8652953655957172

推算一下： $$ I(f) = \int_{0}^{2} \sqrt xdx = \frac{2}{3} x^{\frac{3}{2}}|_0^2 = \frac{2}{3} \times 2^{\frac{3}{2}} = \frac{2}{3}\sqrt 8 $$ 在Python的shell里计算一下：

>>> import numpy as np
>>> 2 * np.sqrt(8) / 3
1.885618083164127

18.3 多重积分

SciPy下的二重积分可以用dblquad函数来计算、三重积分可以用tplquad函数来计算而关于$f(x_1,x_2,\cdots,x_n)$的多重积分可以使用nquad函数。

  • 二重积分dblquad函数来计算，假设有一个函数$f(x, y)$需要计算其二重积分。

$$ I(f(x, y)) = \int_1^2 \int_1^x xydxdy $$ 其高数推算过程如下：

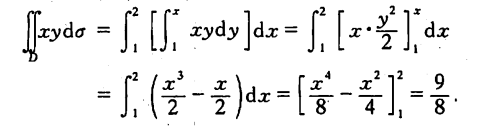
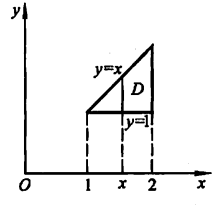
二重积分的各个上下限的含义如下图：

如何用Scipy的dblquad函数呢？ 对于一个泛型的二重积分的一般表达式格式为： $$ I(f(x, y)) = \int_a^b \int_{g(x)}^{h(x)} f(x, y)dxdy $$ 那么dblquad函数的第一个形参应是$f(x,y)$、第2、3、4、5分别是a、b、g(x)、h(x),也就是说dblquad函数的第4和5是一个函数。

from scipy import integrate
import numpy as np
def f(x, y):
    return x * y
def h(x):
    return x
v, err = integrate.dblquad(f, 1, 2, lambda x: 1, h)
print v

程序的执行结果：

1.125

1.125也就是$\frac{9}{8}$。

  • 三重积分可以使用tplquad来计算。三重积分的一般表达式格式为： $$ I(f(x, y)) = \int_a^b \int_{g(x)}^{h(x)} \int^{r(x, y)}_{q(x,y)}f(x, y, z)dxdydz $$ 而tplquad函数调用的形式为：
tqlquad(f, a, b, g, h, q, r)

其中f、g、h、q、r均为函数。下面以计算 $$ I(f(x, y, z)) = \int_{0}^{1} \int_{0}^{\frac{1-x}{2}} \int_{0}^{1-x-2y} xdxdydz $$ 为例，其高数推算过程如下：

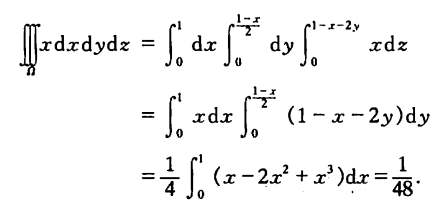
三重积分的各个上下限的含义如下图：

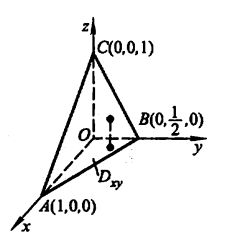
用Python编写的程序如下所示：

from scipy import integrate
import numpy as np
f = lambda x, y, z : x
g = lambda x : 0
h = lambda x : (1 - x) / 2
q = lambda x, y : 0
r = lambda x, y : 1 - x - 2 * y 
v, err = integrate.tplquad(f, 0, 1, g, h, q, r)
print v

程序执行结果：

0.0208333333333

在Python的shell里计算一下$\frac{1}{48}$是多少？

>>> print 1.0 / 48
0.0208333333333

哦，用SciPy的tplquad计算三重积分是如此的简单！

感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持！