14. Scipy Tutorial- 径向基核函数插值

假设函数可以由RBF(Radial basis functions)径向基函数近似表示，把它代入微分方程并且在某个数据点集上在某种度量下迫使微分方程的误差取最小值，从而决定系数$a_i$，甚至点$x_i$，这个方法在一些实际应用领域也获得了非常满意的结果，可视化曲线更具光滑。scipy.interpolate包里有Rbf函数。

• 一元函数的Rbf插值

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import Rbf, splprep
def f(x):
    return x ** 2 + 30 * np.sin(x)

x = np.linspace(-10, 10, 50)
y = f(x)

rf = Rbf(x, y)
x1 = np.linspace(-10, 10, 100)
y1 = rf(x1)

plt.plot(x1, y1, 'r-', x, y, 'bo')
plt.legend(["Radial basis functions", "Orignal pointers"],loc='best')
plt.show()

程序执行结果：

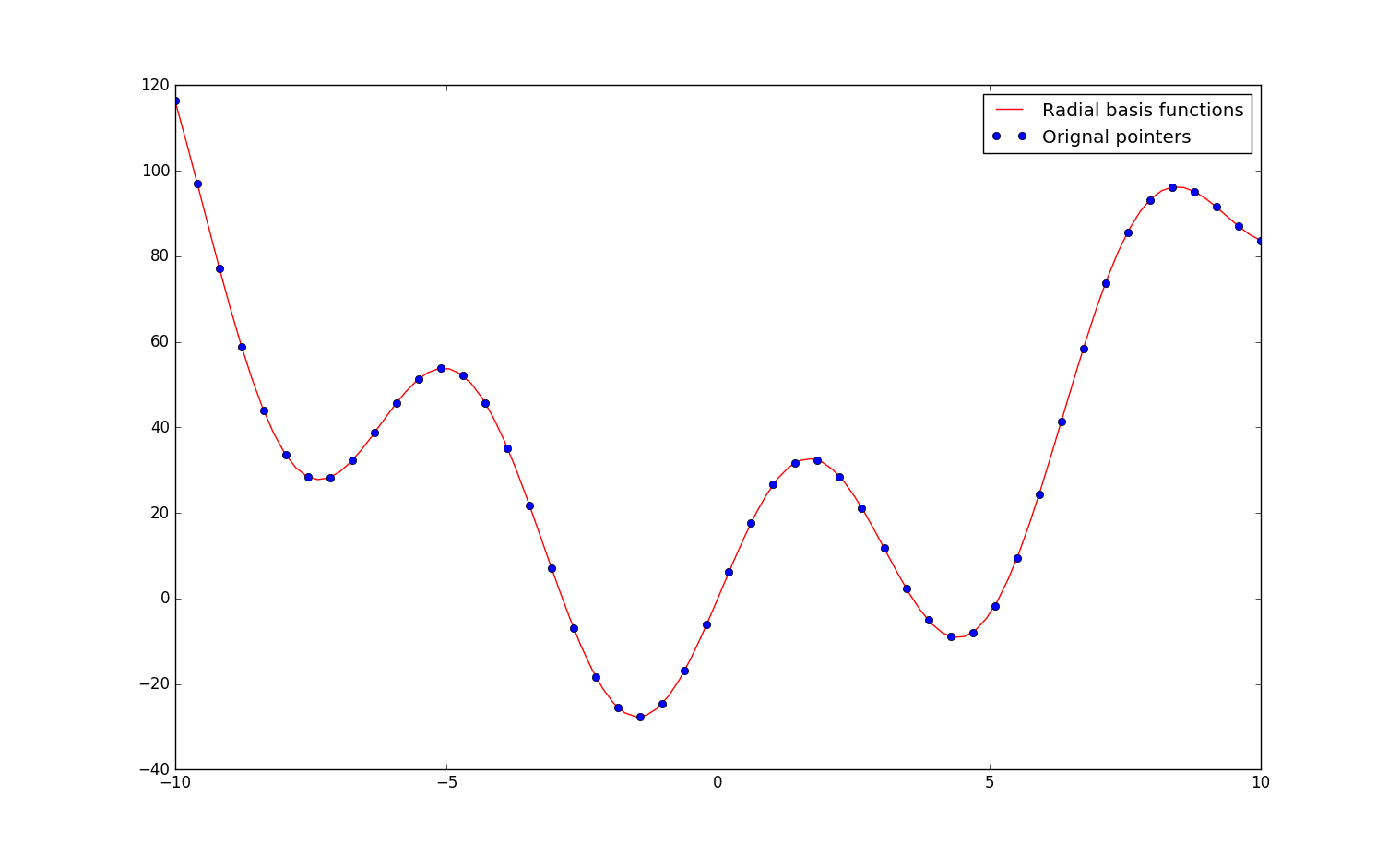Rbf函数基于散点数据$x$和$y$进行插值算法，返回的是一个函数$rf = Rbf(x, y)$，用$rf$计算$x1$各个点的插值即y1 = rf(x1)。

• 二(多)元函数的Rbf插值

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import Rbf, splprep
from matplotlib import cm   
from mpl_toolkits.mplot3d.axes3d import Axes3D

x = np.random.rand(1200) * 4.0 - 2.0
y = np.random.rand(1200) * 4.0- 2.0
z = x * np.exp(-x ** 2 - y ** 2)

rf = Rbf(x, y, z,epsilon = 2)
ti = np.linspace(-2.0, 2.0, 34)
xi, yi = np.meshgrid(ti, ti)
zi = rf(xi, yi)

plt.figure()
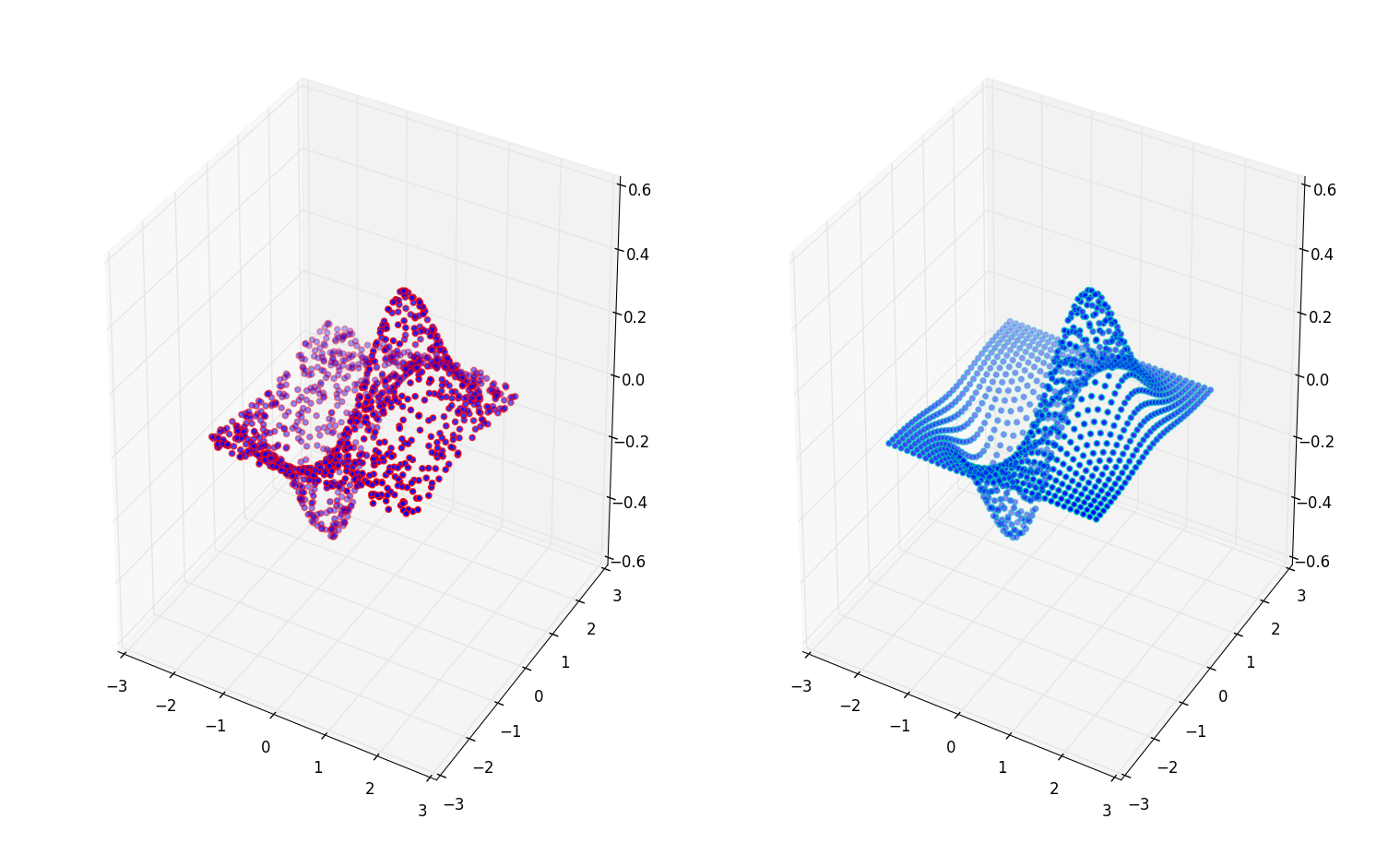
ax1 = plt.subplot2grid((1,2), (0,0), projection='3d')
ax1.scatter(x, y, z, color = 'r')
ax2 = plt.subplot2grid((1,2), (0,1), projection='3d')
ax2.scatter(xi, yi, zi,color = 'c')
plt.tight_layout()
plt.show()

感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持！