Python For Data Analysis-四章第五节

《Python For Data Analysis》的第四章的第五节主要讨论的是NumPy对线性代数的支持函数。

6.1 NumPy矩阵乘法

数组可以看成矩阵，之前介绍过矩阵数组可以基于element-wise规则(同型矩阵对应元素间)直接进行$+-*$和逻辑运算，在学习过《线性代数》(Linear Algebra)通识基础数学课后，可以考虑在NumPy里如何实现两个矩阵的乘法即$x\cdot y$运算。

dot函数可以实现矩阵间乘法。设$A = a_{m\times s}$，$B = b_{s\times n}$，则$A\times B = C$，其中$C = c_{m\times n}$，且 $$ c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots a_{is}b_{sj} = \sum_{k = 1}^{s}a_{ik}b_{kj} $$ 其中$i = 1,2,\cdots,m$，$j = 1,2,\cdots,n$。下面举个例子来使用一下dot函数。

import numpy as np
a = np.array([[1,2,1,0],[-1,0,1,-1]])
b = np.array([[-1,1,1],[2,1,0],[0,0,3],[4,3,-1]])
c = a.dot(b)
print c

执行结果：

[[ 3  3  4]
 [-3 -4  3]]

6.2 NumPy其他矩阵函数

NumPy的linalg模块里提供了很多的和矩阵相关的函数，例如求矩阵的逆矩阵、秩等函数。

inv函数，求矩阵的逆矩阵，要求矩阵是方阵且非奇异($|A|\neq 0 $)。 $$ A^{-1} = \frac{A^{*}}{|A|} $$

import numpy as np
from numpy.linalg import inv, qr
a = np.array([[1,2,3],[1,0,-1],[0,1,1]])
print a, "# a"
b = inv(a)
print b, "# b"

执行结果：

[[ 1  2  3]
 [ 1  0 -1]
 [ 0  1  1]] # a
[[ 0.5  0.5 -1. ]
 [-0.5  0.5  2. ]
 [ 0.5 -0.5 -1. ]] # b

结果对么？由逆矩阵定义知： $$ AA^{-1} = E $$

import numpy as np
from numpy.linalg import inv, qr
a = np.array([[1,2,3],[1,0,-1],[0,1,1]])
print a, "# a"
b = inv(a)
print b, "# b"
print a.dot(b)
print b.dot(a)

执行结果：

[[ 1  2  3]
 [ 1  0 -1]
 [ 0  1  1]] # a
[[ 0.5  0.5 -1. ]
 [-0.5  0.5  2. ]
 [ 0.5 -0.5 -1. ]] # b
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

qr函数，在NumPy部分介绍过了。QR分解法是三种将矩阵分解的方式之一。这种方式，把矩阵分解成一个正交矩阵与一个上三角矩阵的积。QR 分解经常用来解线性最小二乘法问题。 scipy.linalg模块下的qr函数可以对矩阵进行QR分解操作。可以参看示例是调用SciPy的linalg模块的qr函数。
det函数求矩阵的行列式的值。

import numpy as np
from numpy.linalg import inv, qr,det
a = np.array([[1,2,3],[1,0,-1],[0,1,1]])
print a, "# a"
b = inv(a)
print b, "# b"
print det(a)
print det(b)

solve函数求方程组$Ax=b$的根$x$。

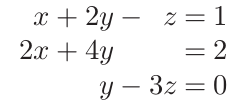
从方程组可得系数矩阵A和b。

import numpy as np
from numpy.linalg import lstsq,solve
a = np.array([[1,2,-1],[2,4,0],[0,1,-3]])
b = b = np.array([1,2,0])
x = solve(a, b)
print x, "# x"

程序执行结果：

[ 1.  0. -0.] # x

lstsq函数，基于least-squares方法求方程组$Ax=b$的根$x$。

import numpy as np
from numpy.linalg import lstsq
a = np.array([[1,2,-1],[2,4,0],[0,1,-3]])
b = b = np.array([1,2,0])
x = lstsq(a, b,rcond=None)[0]
print x, "# x"

程序执行结果：

[1.00000000e+00 7.85316497e-16 4.05562510e-16] # x

解应该是$[1,0,0]$，程序结果和这个值很接近。

感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持！