10. NumPy矩阵运算
本章介绍一些NumPy下的矩阵或者向量的运算函数。
一个行向量乘以一个列向量称作向量的内积,又叫作点积,结果是一个数; 一个列向量乘以一个行向量称作向量的外积,外积是一种特殊的克罗内克积,结果是一个矩阵。
10.1 矩阵的乘法
在Numpy里有很多函数可以实现矩阵的乘法计算。
1). 使用matmul来实现两个矩阵的乘法计算,数学公式如下所示。
$C_{m \times q} = A_{m \times q} \times B_{q \times n}$ 注意两矩阵能相乘,要求A的列等于B的行。
import numpy as np
a = np.arange(1, 7).reshape([2, 3])
b = np.arange(2, 8).reshape([3, 2])
print np.matmul(a, b),"# matmul(a, b)"
程序执行结果如下:
[[28 34]
[64 79]] # matmul(a, b)
2). Numpy里的dot函数也可以对二维及以上的矩阵进行矩阵乘法运算。
import numpy as np
a = np.arange(1, 7).reshape([2, 3])
b = np.arange(2, 11).reshape([3, 3])
print np.matmul(a, b),"# matmul(a, b)"
print a, "# a"
print b, "# b"
print np.dot(a, b), "# dot(a, b)"
程序执行结果:
[[ 36 42 48]
[ 81 96 111]] # matmul(a, b)
[[1 2 3]
[4 5 6]] # a
[[ 2 3 4]
[ 5 6 7]
[ 8 9 10]] # b
[[ 36 42 48]
[ 81 96 111]] # dot(a, b)
从结果可以看出用matmul和dot都能实现对a和b矩阵的乘法计算。
3). 使用NumPy里的inner函数也能实现矩阵的乘法计算。
np.inner(a, b)
inner函数要求形参里的第一个矩阵a和形参里的第二个矩阵b的转置$b^T$ 满足矩阵乘法的要求即a的列等于$b^T$的行。
import numpy as np
a = np.arange(1, 7).reshape([2, 3])
b = np.arange(1, 4).reshape([3, 1])
print np.matmul(a, b),"# matmul(a, b)"
print a, "# a"
print b, "# b"
print np.dot(a, b), "# dot(a, b)"
print "*" * 20
print a, "# a"
b = np.arange(1, 4).reshape([1, 3])
print b, "# b"
print np.inner(a, b), "# inner(a, b)"
程序执行结果:
[[14]
[32]] # matmul(a, b)
[[1 2 3]
[4 5 6]] # a (2, 3)
[[1]
[2]
[3]] # b (3, 1)
[[14]
[32]] # dot(a, b) => (2, 1)
********************
[[1 2 3]
[4 5 6]] # a (2, 3)
[[1 2 3]] # b (1, 3)
[[14]
[32]] # inner(a, b)
注意使用inner的b矩阵的shape是(1, 3)而dot的矩阵b的shape是(3, 1)。
10.1.1 矩阵乘法数学计算过程
1). np.dot(a, b)的数学计算:
2). np.inner(a, b)的数学计算,先将b转置
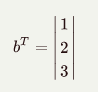
后续和1)一样计算。
10.2 向量的点积(内积)
对于两个一维数组(向量)dot和inner两个数组的计算是对应元素相乘之和作为计算结果值,数学公式如下所示。
$v = a \bullet b = \sum_{i = 0}^{n - 1} a_i \times b_i$
import numpy as np
a = np.arange(1, 7)
b = np.arange(2, 8)
print a, "# a"
print b, "# b"
print np.dot(a, b), "# dot(a, b)"
print np.inner(a, b), "# inner(a, b)"
程序执行结果:
[1 2 3 4 5 6] # a
[2 3 4 5 6 7] # b
112 # dot(a, b)
112 # inner(a, b)
10.3 inner函数总结
多维矩阵a和b的inner内积等价于第一个矩阵乘第二个矩阵b的转置。
10.4 outer函数外积
在理解了inner之后,outer相当于将形参里的第一个矩阵转置乘形参里的第二个矩阵。
import numpy as np
a = np.arange(1, 5)
b = np.arange(2, 5)
print a, "# a"
print b, "# b"
print np.outer(a, b), "# outer(a, b)"
print "*" * 20
a = np.arange(1, 5).reshape((4, 1))
b = np.arange(2, 5).reshape((1, 3))
print a, "# a"
print b, "# b"
print np.matmul(a, b), "# matmul(a, b)"
程序执行结果:
[1 2 3 4] # a
[2 3 4] # b
[[ 2 3 4]
[ 4 6 8]
[ 6 9 12]
[ 8 12 16]] # outer(a, b)
********************
[[1]
[2]
[3]
[4]] # a
[[2 3 4]] # b
[[ 2 3 4]
[ 4 6 8]
[ 6 9 12]
[ 8 12 16]] # matmul(a, b)
10.4.1 outer的数学计算过程
a、b都是行向量: $$ a = \left| \begin{matrix} 1 & 2 & 3 & 4 \end{matrix} \right| $$
$$ b = \left| \begin{matrix} 2 & 3 & 4 \end{matrix} \right| $$
a的转置为:
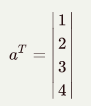
np.outer(a, b)外积则是:
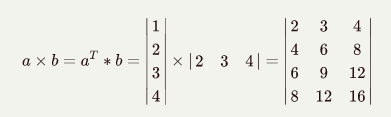
感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持!