Python For Data Analysis-四章第一节
《Python For Data Analysis》的第四章主要讲Python的数组模块numpy,本站有NumPy部分的内容的第一部分即NumPy基础,主要有索引和切片的基础操作,有差异故记之。
2.1 NumPy运算快
众多的Python语言领域里的与科学计算的包对数据的计算通常采用NumPy来存储数据,因为NumPy的array存在于内存,直接内存操作,速度较快。下面的程序测试array和list同样进行对每个数据项乘10次2的操作,测得NumPy存储的数据进行乘2和list数据类型存储的数据乘2的计算速度的对比。
import time, numpy as np
start = time.time()
arr = np.arange(1000000)
print arr
li = list(arr)
print li[:3], li[-3:]
for n in range(10):
arr = arr * 2
print arr
print "array multipy", time.time() - start
start = time.time()
for n in range(10):
li = [x * 2 for x in li]
print li[:3], li[-3:]
print "list multiply", time.time() - start
程序的执行结果:
[ 0 1 2 ... 999997 999998 999999]
[0, 1, 2] [999997, 999998, 999999]
[ 0 1024 2048 ... 1023996928 1023997952 1023998976]
array multipy 0.152561903
[0, 1024, 2048] [1023996928, 1023997952, 1023998976]
list multiply 3.8414721489
从执行结果看出list花去的计算时间较多3.8s而NumPy的数组array进行同样的计算只用了0.15s。缺点是如果array数据较多会消耗大量的内存。
2.2 创建NumPy的Array
在numpy里创立array数据可以有很多的方式,可以将list转为array或者直接调用函数创建array。
- 通过构造函数转化Python基本数据类型为NumPy的array数据类型。
import numpy as np
li = range(10)
print li
arr = np.array(li)
print arr
print type(li), type(arr)
执行结果:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]# print li
[0 1 2 3 4 5 6 7 8 9] # print arr
<type 'list'> <type 'numpy.ndarray'>
程序里的$li$和$arr$都存储了$0\sim 9$共10个数,看似没啥区别,但类型不同。通过调用NumPy的Array的类构造函数,将列表$li$转为Array数据类型数据$arr$。
- 通过NumPy提供的函数创建array。
(1).zeros可以创建全0的array数组。
import numpy as np
li = range(10)
print li
arr = np.array(li)
print arr
print type(li), type(arr)
print np.zeros(5)
print np.zeros((2, 3))
print np.zeros_like(li)
print np.zeros_like(arr)
执行结果:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0 1 2 3 4 5 6 7 8 9]
<type 'list'> <type 'numpy.ndarray'>
[0. 0. 0. 0. 0.]# print np.zeros(5)
[[0. 0. 0.]
[0. 0. 0.]] # print np.zeros((2, 3))
[0 0 0 0 0 0 0 0 0 0] # print np.zeros_like(li)
[0 0 0 0 0 0 0 0 0 0] # print np.zeros_like(arr)
(2).ones可以创建全1的array。
import numpy as np
arr = np.random.randn(2, 3)
print arr
print np.ones(5)
print np.ones((2, 3))
print np.ones_like(arr)
执行结果:
[[-0.05483314 -0.24370693 1.30862163]
[ 0.99580459 0.24697264 1.42776779]]
[1. 1. 1. 1. 1.]
[[1. 1. 1.]
[1. 1. 1.]]
[[1. 1. 1.]
[1. 1. 1.]]
(3). empty创建内存空间没有值(随机很小的值)和full函数创建填充某值的array。
import numpy as np
arr = np.random.randn(2, 3)
print np.empty(5)
print np.empty((2, 3))
print np.empty_like(arr)
print np.full(2, 5)
print np.full((2, 3), 5)
print np.full_like(arr, 5)
print np.full((2, 3), 5, dtype = np.float)
print np.full_like(arr, 5, dtype = np.int8)
程序执行结果:
[0.00000000e+000 6.91625164e-310 2.09332610e-316 2.09329764e-316
2.37151510e-322]
[[6.91625257e-310 6.91625257e-310 2.09332610e-316]
[2.09329764e-316 2.09329764e-316 2.09330239e-316]]
[[6.91625257e-310 6.91625257e-310 2.09332610e-316]
[2.09329764e-316 2.09329764e-316 2.09330239e-316]]
[5 5]
[[5 5 5]
[5 5 5]]
[[5. 5. 5.]
[5. 5. 5.]]
[[5. 5. 5.]
[5. 5. 5.]]
[[5 5 5]
[5 5 5]]
full函数的第一个参数是array的形即shape,第二参数是填充的值。
(4). eye函数可以创建对角线上有数据array。
import numpy as np
print np.eye(3, k = -1)
print np.eye(3, k = 0)
print np.eye(3, k = 1)
print np.eye(3, 4, k = -1)
print np.eye(3, 4, k = 0)
print np.eye(3, 4, k = 2)
执行结果:
[[0. 0. 0.]
[1. 0. 0.]
[0. 1. 0.]]
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
[[0. 1. 0.]
[0. 0. 1.]
[0. 0. 0.]]
[[0. 0. 0. 0.]
[1. 0. 0. 0.]
[0. 1. 0. 0.]]
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]]
[[0. 0. 1. 0.]
[0. 0. 0. 1.]
[0. 0. 0. 0.]]
eye函数第一个参数是行、第二个参数是列,第三个参数k是0表示主对角线,为正表示偏离主对角线之上,为负则在主对角线之下。eye只使用第1个参数创建方阵,等价于identity函数。
2.3 NumPy支持的类型
可以作为array的数据项可以是整形、浮点、字符等类型,通常通过dtype参数来指定数据的类型。
- 整型,Numpy的整形有np.int8、np.int16、np.int32、np.int64等。
- 浮点型,np.float16、np.float32、np.float64。
- 布尔型,bool
- 字符串,string_
- 复数,complex64、complex128、complex256。
可以通过astype函数进行数据项的类型转化。
import numpy as np
a1 = np.array([1, 3, 4], dtype = np.int8)
print a1
a1 = np.array([1, 3, 4], dtype = np.float32)
print a1
print a1.dtype
a2 = a1.astype(np.int8)
print a2
程序执行结果:
[1 3 4]
[1. 3. 4.]
float32
[1 3 4]
2.4 NumPy的算术运算
NumPy的array可以被一个纯数(标量scalar)乘、加等,也可两个同样形状尺寸的数组array直接进行算术运算,规则(element-wise)是两个数组对应位置上数据元素做相应的运算操作作为该位置上的结果。
import numpy as np
a1 = np.array([[1,2,3],[4, 5, 6]], dtype = np.int8)
a2 = np.eye(2,3)
print a1
print a2
print a1 + a2
print a1 * a2
执行结果:
[[1 2 3]
[4 5 6]]
[[1. 0. 0.]
[0. 1. 0.]]
[[2. 2. 3.]
[4. 6. 6.]] # print a1 + a2
[[1. 0. 0.]
[0. 5. 0.]] # print a1 * a2
2.5 NumPy的索引和切片
NumPy的array也支持index和slice操作。
import numpy as np
arr = np.arange(12)
print arr
print arr[2:5]
arr[2:5] = 12
print arr
arr[2:5] = np.arange(3)
print arr
arr[2:5] = [10, 11, 12]
print arr
程序的执行结果:
[ 0 1 2 3 4 5 6 7 8 9 10 11]
[2 3 4]
[ 0 1 12 12 12 5 6 7 8 9 10 11]
[ 0 1 0 1 2 5 6 7 8 9 10 11]
[ 0 1 10 11 12 5 6 7 8 9 10 11]
从程序的执行结果可以看出,如果一个数(标量scalar)赋值给了一个切片需要广播后替换对应切片上的数据,也可以用一个和切片长度相同的array或者list列表来替换切片上的数据。 对于多维数组,只要替换的数据和切片各维上的长度一致,也可被替换。
import numpy as np
arr = np.arange(24).reshape((4, 6))
print arr
print arr[1:3, 2:5]
arr[1:3, 2:5] = np.array([[11,12,13],[21,22,23]])
print arr
程序执行结果:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[ 8 9 10]
[14 15 16]]
[[ 0 1 2 3 4 5]
[ 6 7 11 12 13 11]
[12 13 21 22 23 17]
[18 19 20 21 22 23]]
程序里的reshape函数可以将array进行维度上的变化,最初的arr是一维的数组array,经reshape函数变换后成为$4\times 6$的二维数组了。
2.6 NumPy的布尔索引
首先要说明的是布尔值是可以作为array的数据项的值的,那么由布尔数据组成的数组array可以视为布尔数组。布尔数组$b$可以作为另外一个长度相同的其他数组$a$的索引(和以往的索引为单值不同,是多个布尔值),索引处理a数组里值,从a数组里提取b数组某位置上为真True的a数组对应位置上的数据,作为索引结果集。通俗的说$a[b]$的结果是只返回了b数组为真位置上的a的数据项。
import numpy as np
a = np.array([2, -1, 3, 5, -6])
print a, "# a"
b1 = a > 0
print b1, "# b1"
b2 = np.array([True, False, True, True, False])
print b2, "# b2"
c = np.arange(-5, 5).reshape((5, 2))
print c, "# c"
print c[b2], "# c[b2]"
print c[~(a > 0)], "# c[~(a > 0)]"
print ~(a > 0), "# ~(a > 0)"
程序执行结果:
[ 2 -1 3 5 -6] # a
[ True False True True False] # b1
[ True False True True False] # b2
[[-5 -4]
[-3 -2]
[-1 0]
[ 1 2]
[ 3 4]] # c
[[-5 -4]
[-1 0]
[ 1 2]] # c[b2]
[[-3 -2]
[ 3 4]] # c[~(a > 0)]
[False True False False True] # ~(a > 0)
这里稍微解释一下程序,$a$为由整数组成的数组,$c$也是不过是二维的。$b1$数组是表达式$a > 0$的执行结果,意思是判断数组a的各个位置上的数据项的值是否大于0?得到的$b1$为布尔值组成的数组。 用布尔值组成的数组$b2$可以提取另外一个数组$c$的数据,从c中提取$b2$位置上为True的c同一位置上的数据项。
- 可以用$\&$、$|$来组合复杂的布尔运算。
import numpy as np
a = np.array([2, -1, 3, 5, -6])
print a, "# a"
b1 = (a > 0) & (a < 3)
print b1
b2 = (a > 0) | (a < -3)
print b2
执行结果:
[ 2 -1 3 5 -6] # a
[ True False False False False]
[ True False True True True]
- 通过布尔数组来修改另外一个数组的值,数组a[布尔数组b]这种方式除了作为右值外,即提取a数组的数据,还可以做左值来修改a数组的值。
import numpy as np
a = np.array([2, -1, 3, 5, -6])
print a, "# a"
b = a > 2
print b, "# b"
a[b] = 100
print a, "# a"
程序执行结果:
[ 2 -1 3 5 -6] # a
[False False True True False] # b
[ 2 -1 100 100 -6] # a
2.7 NumPy的Fancy索引
Fancy Indexing,很稀奇的一个名字,在NumPy的官网把这部分定义为高级的index索引技术,这个和Python的索引技术有些类似,Python的索引是单个元素,访问或读写单个数据项,尽管Numpy的数组也支持,如果仅是这样那么array和list就没啥区别了,array支持一次传入多个(整形)索引,一次返回多个数据,这也许就是Fancy之处吧;除此以外对于多维数组也可一次性返回多个数据,以二维数组为例(二维用的比较多),可以给出两组数据,第一组数据给出行坐标、第二组数据给出列坐标,两组数组长度相同,共提取长度个数据,这样就可以确定返回二维数组里那些数据了。
import numpy as np
a = np.arange(12).reshape((3, 4))
print a, "# a"
print a[[0,2]],"# a[[0,2]]"
print a[[0,2], [1, 3]],"# a[[0,2], [1, 3]]"
执行结果:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]] # a
[[ 0 1 2 3]
[ 8 9 10 11]] # a[[0,2]]
[ 1 11] # a[[0,2], [1, 3]]
解释一下表达式a[[0,2], [1, 3]],提取两个数据,坐标为$(0,1)$和$(2,3)$位置上的数据。
2.8 NumPy的数组的转置
转置操作一般是常应用于二维数组,当然高维度的数组也可以进行相应的转置操作。
(1). 对于二维数组可以用.T来实现,也可以用transpose函数实现数组的转置。
import numpy as np
a = np.arange(12).reshape((3, 4))
print a, "# a"
print np.transpose(a)
print a.T
执行结果:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]] # a
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
(2). 对应多维数组,需要给出一个元组来实现数据在轴上的变化。这里,多维数组应用transpose比较复杂,首先明晰一下NumPy的轴的概念,一个简单的记忆是二维以上的数组最外层的方括号的对应的轴号为0,依次内层的方括号所对应的轴号为$1\cdots n - 1$。假设有一个如下的三维数组a:
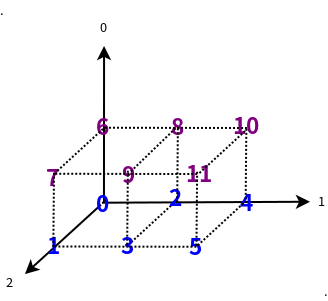
import numpy as np
a = np.arange(12).reshape((2, 3, 2))
print a, "# a"
print a[0,2,1], "# a[0,2,1]"
print a[0],"# a[0]"
print a[0][2],"# a[0][2]"
print a[0][2][1],"# a[0][2][1]"
结果如下:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]] # a
5 # a[0,2,1]
[[0 1]
[2 3]
[4 5]] # a[0]
[4 5] # a[0][2]
5 # a[0][2][1]
- 如果transpose函数传入参数为(1,0,2)意思是说0轴和1轴的数据转置。
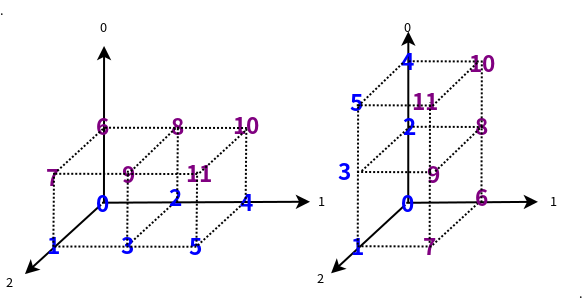
import numpy as np
a = np.arange(12).reshape((2, 3, 2))
print a, "# a"
b = a.transpose((1, 0, 2))
print b,"# a(1,0,2)"
print b[1,0,0],b[1,1,0]
执行结果:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]] # a
[[[ 0 1]
[ 6 7]]
[[ 2 3]
[ 8 9]]
[[ 4 5]
[10 11]]] # a(1,0,2)
2 8
- 如果transpose函数传入参数为(0,2,1)意思是说2轴和1轴的数据转置。
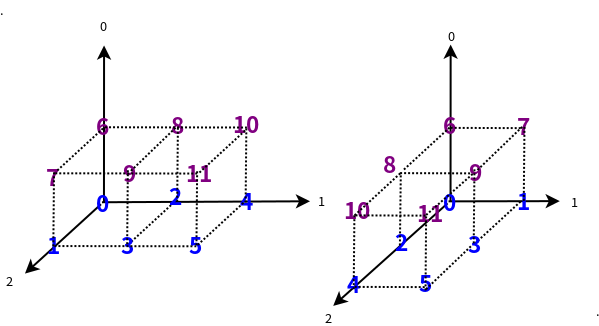
import numpy as np
a = np.arange(12).reshape((2, 3, 2))
print a, "# a"
b = a.transpose((0, 2, 1))
print b, "# a(0, 2, 1)"
print b[1,1,1],b[0,1,2]
执行结果:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]] # a
[[[ 0 2 4]
[ 1 3 5]]
[[ 6 8 10]
[ 7 9 11]]] # a(0, 2, 1)
9 5
- 如果transpose函数传入参数为(2,1,0)意思是说2轴和0轴的数据转置。
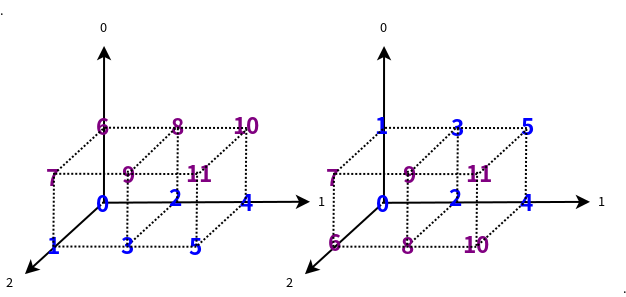
import numpy as np
a = np.arange(12).reshape((2, 3, 2))
print a, "# a"
b = a.transpose((2, 1, 0))
print b, "# a(2, 1, 0)"
print b[0,1,1],b[1,1,1]
执行结果:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]] # a
[[[ 0 6]
[ 2 8]
[ 4 10]]
[[ 1 7]
[ 3 9]
[ 5 11]]] # a(2, 1, 0)
8 9
- 如果transpose函数传入参数为(1,2,0),可以这样去理解:先是$a$数组的2轴和0轴的数据转置得到$a^{'}$即(2,1,0),再对$a^{'}$的0轴和1轴转置得到a的(1,2,0)转置结果。
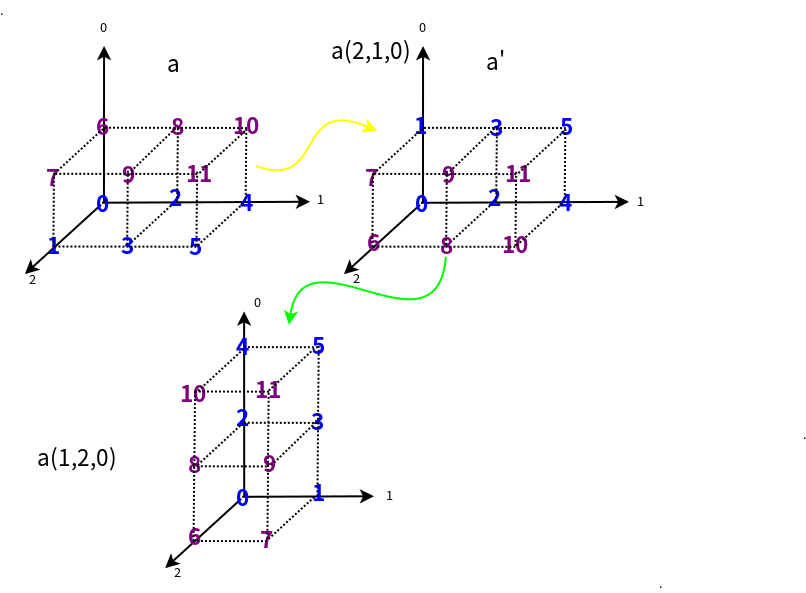
import numpy as np
a = np.arange(12).reshape((2, 3, 2))
print a, "# a"
b = a.transpose((1, 2, 0))
print b, "# a(1, 2, 0)"
print b[0,1,1],b[1,1,1]
执行结果:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]] # a
[[[ 0 6]
[ 1 7]]
[[ 2 8]
[ 3 9]]
[[ 4 10]
[ 5 11]]] # a(1, 2, 0)
7 9
- 而直接对a进行转置,则是和(2,1,0)结果一致。
import numpy as np
a = np.arange(12).reshape((2, 3, 2))
print a, "# a"
b = a.transpose((2, 1, 0))
print b, "# a(2, 1, 0)"
print a.T, "# a.T"
执行结果:
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]] # a
[[[ 0 6]
[ 2 8]
[ 4 10]]
[[ 1 7]
[ 3 9]
[ 5 11]]] # a(2, 1, 0)
[[[ 0 6]
[ 2 8]
[ 4 10]]
[[ 1 7]
[ 3 9]
[ 5 11]]] # a.T
2.9 总结
本章比较难的是多维数组的转置以及对轴的理解。
感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持!