Python For Data Analysis-四章第三节
本章主要内容是介绍基于NumPy数组的Mathematical and Statistical、Sorting、Unique等面向数组的函数。
4.1 NumPy的meshgrid函数
meshgrid函数已经在之前的scipy部分讲解过了,参考1:meshgrid、参考2:mgrid。考虑求$f(x,y)$的应用这里$x \in [a, b]$、$y \in [c, d]$,如何求这个区域里的$f(x,y)$的值呢? 下面以$f(x, y) = x^2 + y^2$其中$x \in {0,1,2,3}$、$y \in {1,2,3}$为例,那么应该计算(0,1)、(0,2)、(0,3)、(1,1)、(1,2)、(1,3)$\cdots$、(3,1)、(3,2)、(3,3)在$f(x, y) = x^2 + y^2$上的各值。可以看出$x$的每个值和$y$的每个值都要算一次。
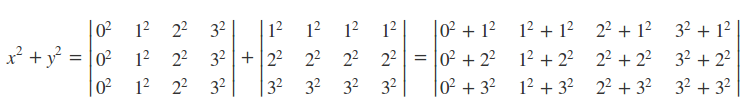
1).当$y = 1$时,$f(0,1) = 0^2+ 1^2 =1$、$f(1,1) = 1^2+ 1^2$、$f(2,1) = 2^2+ 1^2$、$f(3,1) = 3^2+ 1^2$可以表示为下图:

2).当$y = 2$时,$f(0,2) = 0^2+ 2^2 = 4$、$f(1,2) = 1^2+ 2^2$、$f(2,2) = 2^2+ 2^2$、$f(3,2) = 3^2+ 2^2$可以表示为下图:

3).当$y = 3$时,$f(0,3) = 0^2+ 3^2= 9$、$f(1,3) = 1^2+ 3^2$、$f(2,3) = 2^2+ 3^2$、$f(3,3) = 3^2+ 3^2$可以表示为下图:

4).考虑到NumPy的element-wise规则(对应元素做相应的运算操作)。那么以上求解过程可以合并为如下图示:
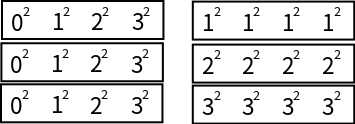
有了上图的两个数组就可以直接利用element-wise规则对两个数组直接使用算术运算了。那么上图的这两个数组可以用meshgrid函数构造出来:
import numpy as np
xpts = np.arange(0, 4, 1)
print xpts, "# xpts"
ypts = np.arange(1, 4, 1)
print ypts, "# ypts"
xs, ys = np.meshgrid(xpts, ypts)
print xs, "# xs"
print ys, "# ys"
执行结果:
[0 1 2 3] # xpts
[1 2 3] # ypts
[[0 1 2 3]
[0 1 2 3]
[0 1 2 3]] # xs
[[1 1 1 1]
[2 2 2 2]
[3 3 3 3]] # ys
那么求$f(x,y) = x^2 + y^2$就可以直接基于xs和ys数组直接运算了。
import numpy as np
xpts = np.arange(0, 4, 1)
print xpts, "# xpts"
ypts = np.arange(1, 4, 1)
print ypts, "# ypts"
xs, ys = np.meshgrid(xpts, ypts)
print xs, "# xs"
print ys, "# ys"
f = xs ** 2 + ys ** 2
print f
执行结果:
[0 1 2 3] # xpts
[1 2 3] # ypts
[[0 1 2 3]
[0 1 2 3]
[0 1 2 3]] # xs
[[1 1 1 1]
[2 2 2 2]
[3 3 3 3]] # ys
[[ 1 2 5 10]
[ 4 5 8 13]
[ 9 10 13 18]]
这也许就是NumPy设计meshgrid函数的意义所在,其主要意图是利用NumPy数组的element-wise规则(对应元素做相应的运算操作)特性来计算。
4.2 NumPy的where函数
where函数的语法格式:
numpy.where(condition[, x, y])
有两种用法:既有条件又有x和y;第二种是只有条件没有x和y。
- 只有条件,返回满足条件的坐标位置。
import numpy as np
a = np.arange(10)
print a, "# a"
from numpy.random import shuffle
shuffle(a)
print a, "# a"
print np.where(a > 5)
执行结果:
[0 1 2 3 4 5 6 7 8 9] # a
[6 1 9 3 0 2 5 4 7 8] # a
(array([0, 2, 8, 9]),)
- 有条件又有x和y,条件为真输出x否则为y。
import numpy as np
a = np.arange(10)
print a, "# a"
from numpy.random import shuffle
shuffle(a)
print a, "# a"
print np.where(a > 5, 1, -1)
执行结果:
[0 1 2 3 4 5 6 7 8 9] # a
[8 9 7 1 4 5 6 2 3 0] # a
[ 1 1 1 -1 -1 -1 1 -1 -1 -1]
4.3 NumPy的统计学相关函数
NumPy提供了一下统计学相关的函数,例如sum、mean、std等。统计学函数的各个语义在pandas部分有解释。
import numpy as np
a = np.arange(10)
print a, "# a"
print np.sum(a), "# np.sum"
print np.cumsum(a), "# np.cumsum"
print np.mean(a), "# np.mean"
print np.std(a), "# np.std"
执行结果:
[0 1 2 3 4 5 6 7 8 9] # a
45 # np.sum
[ 0 1 3 6 10 15 21 28 36 45] # np.cumsum
4.5 # np.mean
2.8722813232690143 # np.std
4.4 NumPy的sort函数
NumPy的sort(升)排序函数是in-place(影响自身不会产生copy)。
import numpy as np
a = np.arange(10)
print a, "# a orginal"
from numpy.random import shuffle
shuffle(a)
print a, "# a shuffle"
a.sort()
print a, "# a sort"
执行结果:
[0 1 2 3 4 5 6 7 8 9] # a orginal
[1 6 0 3 8 2 9 5 7 4] # a shuffle
[0 1 2 3 4 5 6 7 8 9] # a sort
4.5 NumPy的集函数
在NumPy里有一些函数是可以实现两个一维数组的交并集的,即set集函数。有关一些常见集的概念在Python部分有介绍可以复习参阅一下。
- unique求唯一且升序。
import numpy as np
a = np.array([-1, 3, 5, 9, -7, 3, 5])
b = np.array([-2, 3, 3])
print a,"# a"
print b,"# b"
print np.unique(a)
print np.unique(b)
执行结果:
[-1 3 5 9 -7 3 5] # a
[-2 3 3] # b
[-7 -1 3 5 9]
[-2 3]
- in1d函数测试一个数组(第一参数)的各个数据是否在另一数组(第二参数)存在。
import numpy as np
a = np.array([-1, 3, 5, 9, -7, 3, 5])
b = np.array([-2, 3, 3])
print a,"# a"
print b,"# b"
print np.in1d(a, b)
print np.in1d(b, a)
执行结果:
[-1 3 5 9 -7 3 5] # a
[-2 3 3] # b
[False True False False False True False]
[False True True]
- intersect1d函数求交集
import numpy as np
a = np.array([-1, 3, 5, 9, -7, 3, 5])
b = np.array([-2, 3, 3])
print a,"# a"
print b,"# b"
print np.intersect1d(a, b)
print np.intersect1d(b, a)
执行结果:
[-1 3 5 9 -7 3 5] # a
[-2 3 3] # b
[3]
[3]
- union1d函数求并集
import numpy as np
a = np.array([-1, 3, 5, 9, -7, 3, 5])
b = np.array([-2, 3, 3])
print a,"# a"
print b,"# b"
print np.union1d(a, b)
print np.union1d(b, a)
执行结果:
[-1 3 5 9 -7 3 5] # a
[-2 3 3] # b
[-7 -2 -1 3 5 9]
[-7 -2 -1 3 5 9]
- setdiff1d(a, b)属于a但不属于b的集合,差集。
import numpy as np
a = np.array([-1, 3, 5, 9, -7, 3, 5])
b = np.array([-2, 3, 3])
print a,"# a"
print b,"# b"
print np.setdiff1d(a, b)
print np.setdiff1d(b, a)
执行结果:
[-1 3 5 9 -7 3 5] # a
[-2 3 3] # b
[-7 -1 5 9]
[-2]
- setxor1d(a, b)不同属于a和b的集合,对称差集。
import numpy as np
a = np.array([-1, 3, 5, 9, -7, 3, 5])
b = np.array([-2, 3, 3])
print a,"# a"
print b,"# b"
print np.setxor1d(a, b)
print np.setxor1d(b, a)
执行结果:
[-1 3 5 9 -7 3 5] # a
[-2 3 3] # b
[-7 -2 -1 5 9]
[-7 -2 -1 5 9]
4.6 总结
本章难点是对meshgrid函数的理解。
感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持!