10. SciPy最邻近插值

最邻近插值又称插值取样，最简单的图像缩放算法就是最近邻插值(Nearest-neighbors interpolation)。顾名思义，就是将目标图像各点的像素值设为源图像中与其最近的点。效果并不好，放大后的图像有很严重的马赛克，缩小后的图像有很严重的失真这是最邻近插值算法的应用，在SciPy里可以简单理解一下什么是最邻近值插值。

10.1 最邻近插值原理

Nearest-neighbors interpolation简称NN，在机器学习里还有K-NN，和NN类似。最邻近插值法，通常有两组点坐标，类似于图像缩放时原图和放大图的关系，第一组是原图，而第二组坐标则是缩放后的图，原图放大需要填充放大部分的空间的数据，故NN里第二组坐标就是在第一组坐标($x_i, y_i$)间插入的数据，第二组坐标里的$x'_i$是知道的，关键是$y'_i$该是多少合适呢？NN算法在选择每个$x'_i$的$y'_i$时，用第一组坐标里的每个$y_i$作为$y'_i$计算($x'_i, y'_i$)到($x_i, y_i$)间的距离$d$,取最小$d$时的$y_i$最为这个$x'_i$的$y'_i$值。假设第一组坐标($x_i, y_i$)有5个，那么$d$就该有25个值，如下图所示：

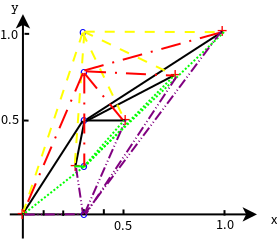
上图是$x'_i = 0.3$时计算$y'_i =$分别取$ {0.0,0.25,0.5,0.75,1.0}$到第一组各个点$(0.0,0.0),(0.25,0.25),(0.5,0.5),(0.75,0.75),(1.0,1.0)$之间的距离。经计算第二组$(x'_i, y'_i) $为$ (0.3, 0.25)$的点到第一组各个点距离最小的是$(x_i, y_i) $为 $(0.25, 0.25)$的点，即图上绿色横线。那么此时第一组$(x_i, y_i) $为 $(0.25, 0.25)$的$y_i=0.25$值作为第二组$(x'_i, y'_i) $坐标点$y'_i$的值，即$y'_i = 0.25$。选择$(x'_i, y'_i) $为$ (0.3, 0.25)$的点作为$x'_i = 0.3$处最邻近NN插值算法的插值点坐标，这就是最邻近插NN算法。

上图用Python程序实现的代码如下：

import numpy as np, matplotlib.pyplot as plt
from scipy.interpolate import interp1d
xi = np.linspace(0, 1, 11, endpoint=True)
vi = np.linspace(0, 1, 5, endpoint=True)
#yi = np.array([8,2,6,2,4])
def fv(x):
    return x
interp_nn = interp1d(vi, fv(vi), kind='nearest')    
#interp_nn = interp1d(vi, yi, kind='nearest')   
print xi,"#xi"
print fv(xi), "fv(xi)"
print vi, "#vi"
print fv(vi), "fv(vi)"
xy = fv(xi)
vy = fv(vi)
print xy, "#xy"
print vy, "#vy"
def distance(ax, ay, bx, by):
    for i in range(len(ax)):
        tt = list()
        for j in range(len(bx)):
            for k in range(len(bx)):
                d = np.sqrt(np.power(ax[i] - bx[k],2) + np.power(by[j] - by[k],2))
                tt.append((d, k))
        ret = sorted(tt, key = lambda x : x[0])
        print "y' is", by[ret[0][1]]

print interp_nn(xi),"#interp_nn(xi)"
distance(xi, xy, vi, vy)
#distance(xi, xy, vi, yi)
plt.plot(vi, fv(vi), 'b+', markersize=18)
#plt.plot(vi, yi, 'b+', markersize=18)
plt.plot(xi, interp_nn(xi), 'ro')
plt.ylim(-0.05, 1.05)
plt.xlim(-0.05, 1.05)
plt.show()

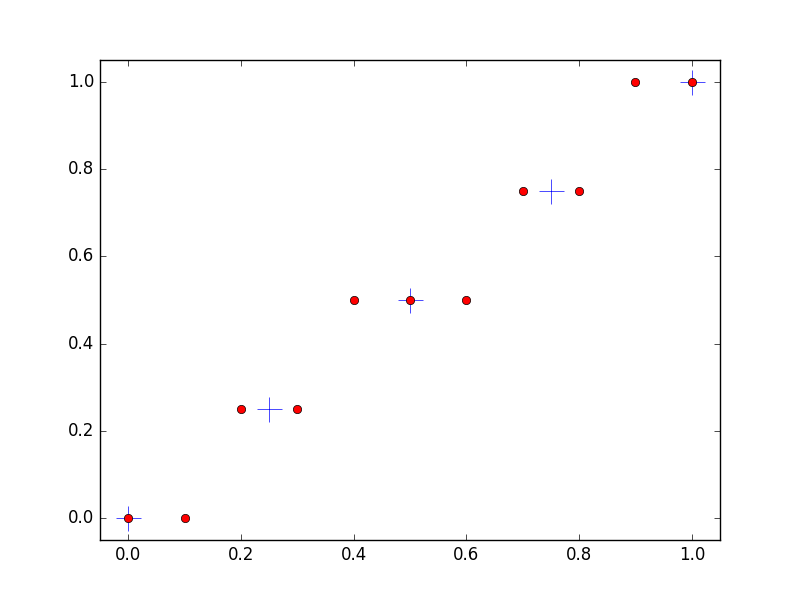
程序执行结果：

[ 0.   0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9  1. ] #xi
[ 0.   0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9  1. ] fv(xi)
[ 0.    0.25  0.5   0.75  1.  ] #vi
[ 0.    0.25  0.5   0.75  1.  ] fv(vi)
[ 0.   0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9  1. ] #xy
[ 0.    0.25  0.5   0.75  1.  ] #vy
[ 0.    0.    0.25  0.25  0.5   0.5   0.5   0.75  0.75  1.    1.  ] #interp_nn(xi)
y' is 0.0
y' is 0.0
y' is 0.25
y' is 0.25
y' is 0.5
y' is 0.5
y' is 0.5
y' is 0.75
y' is 0.75
y' is 1.0
y' is 1.0

$y'$输出值为每个$x'$选择插值$y'$坐标值。 distance函数为计算每个$x'_i$选择$y_i$作为$y'_i$到各个$(x_i, y_i)$点的距离，$sorted$函数对结果里的距离数据(key = lambda x : x[0])升序排序,$by[ret[0][1]]$代表距离最小的$(x_i, y_i)$点的$y_i$值，作为$y'_i$的值。 distance函数里的i循环是针对每个$x'_i$从$y_i$找到其最邻近插值算法的$y'_i$的值，j循环的作用是让$x'_i$的$y'_i$取第一组坐标的$y_i$，k循环则是计算$y'_i$取值为各个$y_i$时的距离$d$。有关interp1d函数看下一节。

10.2 最邻近插值应用

scipy.interpolate模块下的interp1d函数的形参kind设置成nearest可以实现最邻近插值算法。

import numpy as np, matplotlib.pyplot as plt
from scipy.interpolate import interp1d
v = np.linspace(0, 1, 5)
print v
def f(x):
    return np.sin(3 * x)
xi = np.linspace(0, 1, 100)
print xi, "#xi"
interp_nn = interp1d(v, f(v), kind='nearest')
print interp_nn(xi)
plt.plot(v, f(v), 'g')
plt.plot(xi, f(xi), 'b*')
plt.plot(xi, interp_nn(xi), 'ro')
plt.title("Nearest-neighbor approximation")
plt.ylim(-0.05, 1.05)
plt.xlim(-0.5, 1.05)
plt.show()

程序执行结果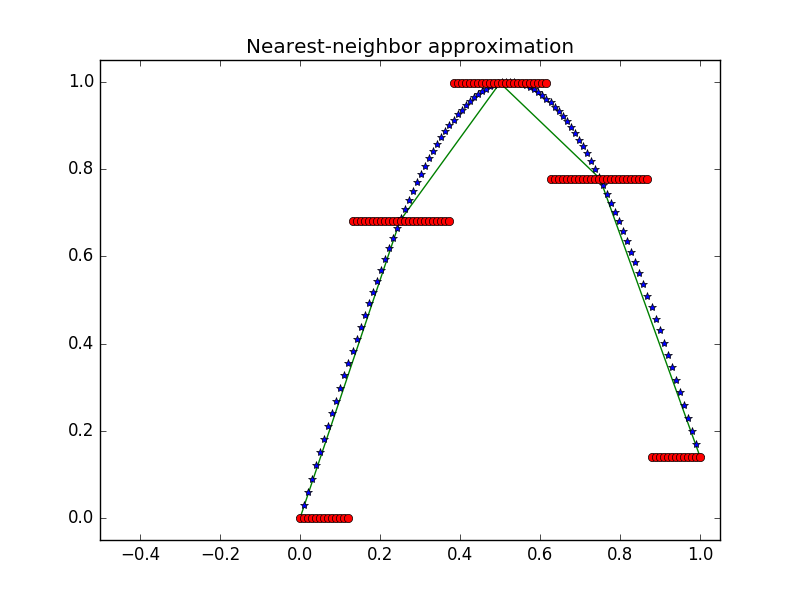： scipy.interpolate模块下的interp1d函数可以进行一元插值，不同的scipy版本支持的插值算法个数不同，本程序基于scipy-0.17.1版本，所支持的interp1d可以从其官方文档查找到,有 ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic, ‘cubic’ where ‘slinear’, ‘quadratic’ and ‘cubic’等类型。其第一个形参和第二个形参长度要求相等，可以理解为图像缩放的原图，即第一组坐标，供后续插值作为参考，kind形参赋值所要使用的插值算法，本章研究的是最邻近插值故kind = nearest。interp1d函数的返回值是类似于C语言里的函数指针的概念的变量值，可以后用圆括号传入参数即interp_nn(xi)用于寻找xi这些坐标点里$x'_i$集合最邻近插值的各个$x'_i$的$y'_i$。

感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持！