9. Scipy Tutorial-方程(组)求解(根)

在scipy里利用root函数可以比较容易的获得多项式方程的根，即求解方程式。

import numpy as np
from scipy import optimize
x = np.arange(-10, 10, 0.1)
def f(x):
    return x ** 2 + 30 * np.sin(x)
grid = (-10, 10, 0.1)
xmin_global = optimize.brute(f, (grid, ))
print "Global minima found ", xmin_global
xmin_local = optimize.fminbound(f, 0, 10)
print "Local minimum found ", xmin_local
root = optimize.root(f, [-3.5, 0, 3.5, 6])
print "root is:",
for x1 in root.x:
    print x1,
print ""
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6, 4))
ax = fig.add_subplot(111)
ax.plot(x, f(x), 'b-', label="f(x)")
xmins = np.array([xmin_global[0], xmin_local])
ax.plot(xmins, f(xmins), 'go', label="Minima")
ax.plot(root.x, [0.0] * len(root.x), 'kv', label="Roots")
ax.legend(loc='best')
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax.axhline(0, color='gray')
plt.show()

执行结果：

Global minima found  [-1.47246094]
Local minimum found  4.413720288458936
root is: -2.8645419447440807 0.0 3.584078604649768 5.1777791153176365

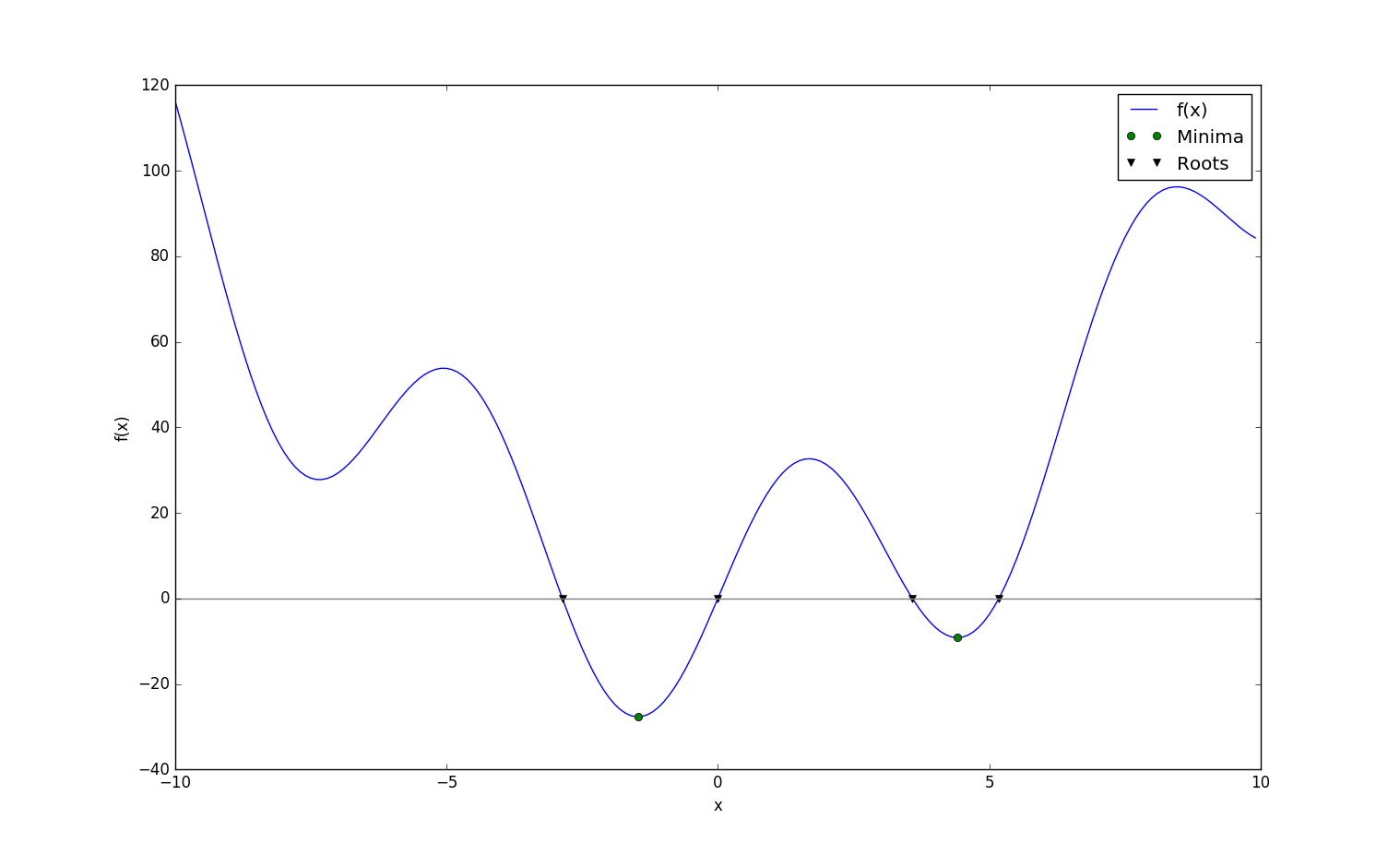scipy下的optimize模块里的brute函数是尝试用暴力破解(brute force)的方法去获得某区域内(这里通过grid给出)最小值，缺点是消耗大量的内存运算速度慢。 scipy下的optimize模块里的fminbound函数可以获得某区域内的极小值，需要给出$x_0$起点和$x_1$终点。类似的函数还有golden、brentq、brent、bracket等。而root函数可以函数f的根。

scipy.optimize.root(fun, x0, args=(), method='hybr'...)

root函数的第一个参数fun是要求传入要求解的方程，$x_0$是函数fun的第一个参数，其余参数可放在$args$里。调用root函数时fun被赋值为函数$f$，而函数$f$只有一个参数，故args无需指定。

方程组的求根(解)。只需要定一个返回多个表达式的函数$f(x)$即可，每个表达式代表一个$f_i(x) = 0$的方程。例如求下面的方程组，请注意如何定义$f$函数的。 $$ 5x_0 + x_1 + 2x_2 = 21 \Longrightarrow f_0(x) = 5x_0 + x_1 + 2x_2 - 21 = 0 $$ $$ 3x_0 + 8x_1 - 4x_2 = -23 \Longrightarrow f_1(x) = 3x_0 + 8x_1 - 4x_2 +23 = 0 $$ $$ -3x_0 + 2x_1 + 7x_2 = 15\Longrightarrow f_2(x)=-3x_0 + 2x_1 + 7x_2 - 15 = 0 $$

import numpy as np
from scipy import optimize
x = np.arange(-10, 10, 0.1)
def f(x):
    return 5*x[0] + x[1] + 2 * x[2] - 21, 3 * x[0] + 8 * x[1] - 4 *x[2] + 23, -3*x[0] + 2 * x[1] + 7 *x[2] -15

print 'hybr',"-"* 20
ret = optimize.root(f,[0,1, 3],method='hybr')
print ret
print 'Krylov',"-" * 20
ret = optimize.root(f,[0,1, 3],method='Krylov')
print ret
print 'broyden2',"-" * 20
ret = optimize.root(f,[0,1, 3],method='broyden2')
print ret

程序执行结果：

hybr --------------------
  status: 1
 success: True
     qtf: array([-1.23090561e-11,  5.03477212e-11, -1.63889212e-11])
    nfev: 6
       r: array([-6.55743852, -3.50746712,  3.50746712, -7.52978581,  0.49107299,
       -7.5137555 ])
     fun: array([ 0.00000000e+00,  3.55271368e-15, -1.77635684e-15])
       x: array([ 3., -2.,  4.])
 message: 'The solution converged.'
    fjac: array([[-0.76249285, -0.45749571,  0.45749571],
       [ 0.22237267, -0.84934007, -0.47871895],
       [-0.60758131,  0.26328523, -0.74935028]])
Krylov --------------------
  status: 1
 success: True
     fun: array([-3.99883575e-08, -1.63128123e-06,  1.59275904e-06])
       x: array([ 2.99999992, -2.00000007,  4.00000021])
 message: 'A solution was found at the specified tolerance.'
     nit: 2
broyden2 --------------------
  status: 1
 success: True
     fun: array([-7.10542736e-15, -7.10542736e-15,  3.55271368e-15])
       x: array([ 3., -2.,  4.])
 message: 'A solution was found at the specified tolerance.'
     nit: 7

method='Krylov'适合变量较多的方程(组)的求根，速度要比method='hybr'(root函数默认求根方式)快，原因是root函数求根时设置method='Krylov'，其内部使用了雅克比迭代法求根。

感谢Klang(金浪)智能数据看板klang.org.cn鼎力支持！